قاعدة 3 (la regle de 3)



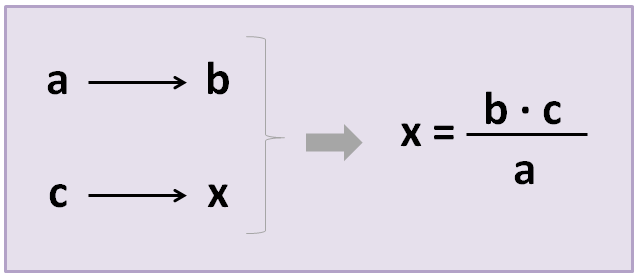

أحد أكثر الشكوك شيوعًا التي يسألنا عنها الأطفال هو قاعدة 3 (la regle de 3):
لماذا ، متى يجب استخدامها ، كيف يتم ذلك ...
سنستفيد من مشاركة اليوم لمراجعة قاعدة 3 من خلال الإدخالات السابقة. آمل أن يساعدك على حل كل شكوكك!
يتم استخدام قاعدة 3 لحل مشاكل التناسب ، المباشرة والعكسية.
لذلك سنبدأ بشرح ما هو التناسب المباشر والتناسب العكسي.
يمكن أن تكون الأحجام النسبية متناسبة بشكل مباشر أو متناسبة عكسيًا .
- تكون متناسبة بشكل مباشر عندما يزيد مقدار على مقدار الآخر بشكل متناسب . بمعنى ، إذا ضربنا أو قسمنا أحدهما في أو على رقم معين ، فإن الآخر أيضًا يتم ضربه أو قسمة على نفس العدد .
فيما يلي مثال على التناسب المباشر: ما العلاقة التي يمكننا رؤيتها بين عدد الموز وعدد الصناديق التي نحتاجها لتخزينه
صورة
يمكنك أن تلاحظ أنه كلما أضفنا الموز سنحتاج للمزيد من العلب . هذان الكميتان (كمية ابلموز ز كمية العلب ) متناسبتان بشكل مباشر .
فيما يلي مثال على التناسب العكسي: كلما زادت سرعة سيارة السباق ، قل الوقت الذي تستغرقه لف دورة السباق.


- إذا سارت بسرعة 50 كم / ساعة فستستغرق 24 دقيقة
- إذا سارت بسرعة 100 كم / ساعة فستستغرق 12 دقيقة: ضعف السرعة (50 × 2 = 100) فستستغرق النصف (24/2 = 12)
- إذا سارت بسرعة 200 كم / ساعة فستستغرق 6 دقائق: أسرع 4 مرات (50 × 4 = 200) وستستغرق 4 مرات أقل (24/4 = 6)
- إذا كانت سرعتها 300 كم / ساعة ، فإنها تستغرق 4 دقائق: أسرع 6 مرات (50 × 6 = 300) وستستغرق أقل 6 مرات (24/6 = 4)
يمكنك أن ترى أنه كلما زادت سرعة سيارة السباق ، كلما قل الوقت الذي يستغرقه إكمال دورة أو لف الدائرة ، أليس كذلك؟ تحافظ هاتان الكميتان على علاقة عكسية أو متناسبة بشكل عكسي.
تظهر العلاقات النسبية بشكل متكرر في حياتنا اليومية. هل من الممكن أعطائنا أمثلة ؟
ما هي القاعدة البسيطة لـ 3؟
قاعدة " 3 " هي عملية تساعدنا على الحل السريع لمسائل تتعلق بالتناسب المباشر و العكسي .
لإنشاء قاعدة 3 بسيطة ، نحتاج إلى 3 بيانات :
مقداران ( أي حدان ) يتناسبان مع بعضهما البعض ( أ ، ب ) و مقدار (حد) ثالث ( ج ). و من خلال هاته الثلاث مقادير ينكتشف الحد الرابع للتناسب .
قاعدة التناسب المباشر البسيط :
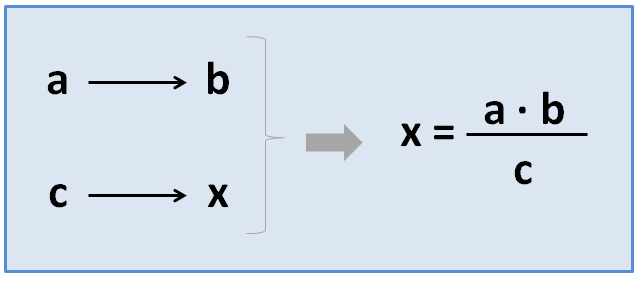
- القاعدة المطبقة في حالات التناسب المباشر . نضع في الجدول البيانات الثلاثة ( أ ، ب ، ج ) والمجهول ، أي البيانات التي نريد اكتشافها ( س ). ثم سنطبق الصيغة التالية:
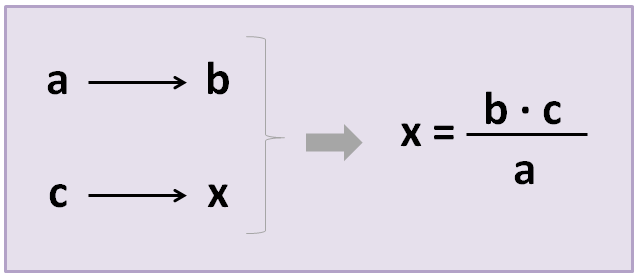
في مثال الموز و العلب :
3 → 1
6 → س
س = (1 × 6) / 3 = 2
القاعدة العكسية البسيطة : تطبق القاعدة 3 البسيطة في حالات التناسب العكسي . سنضع في الجدول البيانات الثلاثة ( أ ، ب ، ج ) والمجهولة ، أي البيانات التي نريد اكتشافها ( س ) ، تمامًا كما وضعناها في الحالة السابقة . لكن تطبيق صيغة مختلفة :

في مثال السيارة على المسار
50 ← 24
100 → س
س = (50 × 24) / 100 = 12
نتمنى أن تكون قد تعرفت بالفعل كيفية حل القاعدة 3 البسيطة المباشرة والقاعدة 3 البسيطة المعكوسة أليس ذلك سهل جدا؟
هل أعجبك هذا الدرس ؟ هل أجاب على تساؤلاتك ؟



ليست هناك تعليقات:
إرسال تعليق